关于指针
在最开始的开始我们必须先搞清楚指针这个c语言中最具特色的工具,而数据结构中的诸多结构都用到了指针,我个人是这样理解的:
- 指针就像是一张存储卡一样,比如我们拿走一个a变量的存储卡(指针),即便换了任意一个变量,我们只要将存储卡(指针)更新到新的变量中,我们访问的数据仍旧是原来
的那个变量a中的数据。
指针的比喻
1. 指针是地址的代表
- 在内存中,每个变量都占用一个存储空间,并且每个存储空间都有一个地址。指针实际上并不是直接存放数据,而是存放某个变量在内存中的地址。
- 你可以将指针比作某个特定位置的“地址标签”,而这个位置存放的是实际的数据。
2. 更新指针指向的对象
- 如果你有一个指针
p 指向某个变量 x,通过 *p(假设 p 是 int* 类型)可以访问 x 的值。此时,你可以认为指针像是指向存储卡的标签,指向某个特定存储区。
- 如果你把指针
p 指向另一个变量 y,那么通过 *p 就可以访问变量 y 的值,即使之前指向的是 x。换句话说,虽然 p 指针本身是改变了指向的对象,但指针所指向的值也是随之更新的。
3. 对指针的理解
指针的赋值: 当前指针 p 指向的地址可以改变,例如 p = &y;。这只是更新了指针指向,即“存储卡的标签”。p 现在指向的新地址(y 的地址)中的值会通过 *p 访问到,因而能够读取不同的数据。
临时性与持久性: 重要的是要理解指针所指向的内容(数据)在内存中可能是临时的,也可能是持久的,具体取决于数据的生命周期。比如,当一个变量超出作用域时,该指针不再有效,访问它可能导致未定义行为(类似于拿着已不存在标签的卡)。
顺序表—— Sequence List
一、顺序表的定义
顺序表:线性表的顺序存储,它是用一组地址连续的存储单元依次存储线性表中的数据元素,使得逻辑上相邻的两个元素在物理位置上也相邻。
二、顺序表的特点
①随机访问:可直接通过下标访问
②存储密度高:每个节点只能存数据元素
③拓展容量不方便:即便采用动态分配方式,迁移数据时时间复杂度也比较高
④插入、删除操作不方便:需要移动大量元素
三、顺序表的实现方式
实现方式:静态分配和动态分配
四、静态分配的顺序表上的操作
静态分配的顺序表的优缺点
缺点:顺序表的表长确定后无法修改,存满了就存不了了
顺序表的类型描述
1
2
3
4
5
| #define MaxSize 10;
typedef struct{
int data[MaxSize];
int length;
}SqList;
|
初始化
1
2
3
4
5
6
7
|
void InitList(SqList &L){
for(int i=0; i<MaxSize; i++){
L.data=[i]=0;
}
L.length=0;
}
|
插入
1
2
3
4
5
6
7
8
9
10
11
|
bool ListInsert(SqList &L, int i,int e){
if(i<1||i>L.length+1)
return false;
if(L.length>=MaxSize)
return false;
for(int j=L.length; j>=i; j--)
L.data[j]=L.data[j-1];
L.data[i-1]=e;
L.length++;
}
|
插入的时间复杂度:
最好情况:插到表尾,不需移动元素,循环0次,最好时间复杂度=O(1)
最坏情况:插到表头,移动n个元素,循环n次,最坏时间复杂度=O(n)
平均情况:设插入概率为p=1/n+1,则循环np+(n-1)p+…+1p=n/2,平均时间复杂度=O(n)
删除
1
2
3
4
5
6
7
8
9
10
11
12
13
|
bool ListDelete(SqList &L, int i,int &e){
if(i<1||i>L.length+1){
return false;
}else{
e = L.data[i-1];
for(int j=i; j<L.length; j++){
L.data[j]=L.data[j-1];
}
L.length--;
return ture;
}
}
|
删除的时间复杂度:
最好情况:删除表尾,不需移动元素,循环0次,最好时间复杂度=O(1)
最坏情况:删除表头,移动n-1个元素,循环n次,最坏时间复杂度=O(n)
平均情况:设删除概率为p=1/n,则循环(n-1)p+(n-2)p+…+1p=(n-1)/2,平均时间复杂度=O(n)
查找
按位查找
1
2
3
4
|
int GetElem(Sqlist L, int i){
return L.data[i-1];
}
|
按位查找的时间复杂度
时间复杂度=O(1)
按值查找
1
2
3
4
5
6
7
8
|
int LocateElem(Sqlist L, int e){
for(int i=0; i<L.length; i++){
if(L.data[i] == e)
return i+1;
}
return -1;
}
|
按值查找的时间复杂度
最好情况:目标在表头,循环1次,最好时间复杂度=O(1)
最坏情况:目标在表尾,循环n次,最坏时间复杂度=O(n)
平均情况:设删除概率为p=1/n,则循环(n-1)p+(n-2)p+…+1p=(n+1)/2,平均时间复杂度=O(n)
无销毁
系统自动销毁
五、动态分配的顺序表上的操作
动态分配的顺序表的优缺点:
优点:可以动态增加长度
缺点:动态增加长度中的迁移工作时间开销大
顺序表的类型描述
1
2
3
4
5
| typedef struct{
int *data;
int MaxSize;
int length;
}SqList;
|
初始化
1
2
3
4
5
6
7
|
void InitList(SqList &L){
L.data=(int *)malloc(InitSize*sizeof(int));
L.MaxSize=InitSize;
L.length=0;
}
|
动态增加数组长度
方法:借用一个指针指向原来顺序表,新建一个更大的顺序表,将原数据迁移过来,并更改顺序表大小,最后释放原顺序表空间
1
2
3
4
5
6
7
8
9
10
|
void IncreaseSize(SqlList &L, int len){
int *p=L.data;
L.data=(int *)malloc((L.InitSize+len)*sizeof(int));
for(int i=0; i<L.length; i++){
L.data[i]=p[i];
}
L.MaxSize=L.MaxSize+len;
free(p);
}
|
插入
在静态分配的基础上,如果容量不够,则动态增加
1
2
3
4
5
6
7
8
9
10
11
|
bool ListInsert(SqList &L, int i,int e){
if(i<1||i>L.length+1)
return false;
if(L.length>=MaxSize)
IncreaseSize(L,10);
for(int j=L.length; j>=i; j--)
L.data[j]=L.data[j-1];
L.data[i-1]=e;
L.length++;
}
|
插入的时间复杂度:
最好情况:插到表尾,不需移动元素,循环0次,最好时间复杂度=O(1)
最坏情况:插到表头,移动n个元素,循环n次,最坏时间复杂度=O(n)
平均情况:设插入概率为p=1/n+1,则循环np+(n-1)p+…+1p=n/2,平均时间复杂度=O(n)
删除(与静态一样)
1
2
3
4
5
6
7
8
9
10
11
12
13
|
bool ListDelete(SqList &L, int i,int &e){
if(i<1||i>L.length+1){
return false;
}else{
e = L.data[i-1];
for(int j=i; j<L.length; j++){
L.data[j]=L.data[j-1];
}
L.length--;
return ture;
}
}
|
删除的时间复杂度:
最好情况:删除表尾,不需移动元素,循环0次,最好时间复杂度=O(1)
最坏情况:删除表头,移动n-1个元素,循环n次,最坏时间复杂度=O(n)
平均情况:设删除概率为p=1/n,则循环(n-1)p+(n-2)p+…+1p=(n-1)/2,平均时间复杂度=O(n)
查找(与静态一样)
按位查找
1
2
3
4
|
int GetElem(Sqlist L, int i){
return L.data[i-1];
}
|
按位查找的时间复杂度
时间复杂度=O(1)
按值查找
1
2
3
4
5
6
7
8
|
int LocateElem(Sqlist L, int e){
for(int i=0; i<L.length; i++){
if(L.data[i] == e)
return i+1;
}
return -1;
}
|
按值查找的时间复杂度
最好情况:目标在表头,循环1次,最好时间复杂度=O(1)
最坏情况:目标在表尾,循环n次,最坏时间复杂度=O(n)
平均情况:设删除概率为p=1/n,则循环(n-1)p+(n-2)p+…+1p=(n+1)/2,平均时间复杂度=O(n)
销毁
1
2
3
4
5
6
7
|
void DestroyList(Sqlist &L){
free(L.data);
L.length = 0;
L.MaxSize = 0;
L.data = nullptr;
}
|
六、共同的操作
求表长
1
2
3
4
|
int Length(Sqlist L){
return L.length;
}
|
遍历
1
2
3
4
5
6
7
|
void PrintList(Sqlist L){
for(int i=0; i<L.length; i++){
cout<<L.data[i]<<" ";
}
cout<<endl;
}
|
判空
1
2
3
4
|
int Empty(Sqlist L){
return L.length==0? 1 : 0;
}
|
七、完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
|
#include<bits/stdc++.h>
using namespace std;
#define MaxSize 100
typedef struct Sqlist{
int data[MaxSize];
int length;
}Sqlist;
void Init(Sqlist &L){
L.length = 0;
}
int Length(Sqlist L){
return L.length;
}
void Insert(Sqlist &L, int i, int x){
if(i<1 || i>L.length+1 || L.length >= MaxSize){
cout<<x<<" Insert failed."<<endl;
return;
}
for(int j=L.length; j>=i; j--){
L.data[j] = L.data[j-1];
}
L.data[i-1]=x;
L.length++;
}
void PrintList(Sqlist L){
cout<<"L: ";
for(int i=0; i<L.length; i++){
cout<<L.data[i]<<" ";
}
cout<<endl;
}
int LocateElem(Sqlist L, int x){
for(int i=0; i<L.length; i++){
if(L.data[i] == x)
return i+1;
}
return -1;
}
int GetElem(Sqlist L, int i){
return L.data[i-1];
}
int Delete(Sqlist &L, int i, int &x){
if(i<1 || i>L.length){
return -1;
}else{
x = L.data[i-1];
for(int j=i; j<L.length; j++){
L.data[j-1] = L.data[j];
}
L.length--;
return x;
}
}
int Empty(Sqlist L){
return L.length==0? 1 : 0;
}
int main(){
Sqlist L;
Init(L);
Insert(L, 1, 50);
Insert(L, 2, 60);
Insert(L, 1, 40);
Insert(L, 1, 666);
Insert(L, 5, 70);
Insert(L, 6, 40);
Insert(L, 7, 100);
cout<<"长度:"<<Length(L)<<endl;
PrintList(L);
int x;
cout<<"第三个元素是:"<<GetElem(L,3)<<endl;
cout<<"40在第"<<LocateElem(L,40)<<"位"<<endl;
cout<<"删除"<<Delete(L,6,x)<<endl;
PrintList(L);
if(!Empty(L)){
cout<<"L不为空"<<endl;
}else{
cout<<"L为空"<<endl;
}
return 0;
}
|
单链表—— Singly Linked List
一、单链表的定义
单链表:线性表的链式存储,它是通过一组任意的存储单元来存储线性表中的数据元素,不需要使用地址连续的存储单元,因此它不要求在逻辑上相邻的两个元素在物理位置上也相邻。
二、单链表的特点
①不能随机访问:遍历查找访问
②存储密度不高:每个节点既要存数据元素又要存指针
③拓展容量方便:直接用建立单链表拓展
④插入、删除操作方便:知道位置直接插入和删除
三、单链表的实现方式
实现方式:不带头结点和带头结点,一般带头结点比不带头结点好
带头结点:写操作代码方便,一般用带头结点,不明确的都是带头结点的
不带头结点:写操作代码麻烦,要区分第一个数据和后续数据的处理
注:这两种方式主要是:类型描述相同,初始化和判空不同
四、单链表上的操作
单链表的类型描述
1
2
3
4
| typedef struct LNode{
int data;
struct LNode *next;
}LNode, *LinkList;
|
不带头结点的初始化和判空
1
2
3
4
5
|
void InitList(LinkList &L){
L = NULL;
L->next = NULL;
}
|
1
2
3
4
5
6
7
8
|
bool Empty(LinkList L){
if(L == NULL){
return true;
}else{
return false;
}
}
|
带头结点的初始化和判空
1
2
3
4
5
|
void InitList(LinkList &L){
L = (LNode *)malloc(sizeof(LinkList));
L->next = NULL;
}
|
1
2
3
4
5
6
7
8
|
bool Empty(LinkList L){
if(L->next == NULL){
return true;
}else{
return false;
}
}
|
建立单链表
头插法建立单链表
用于链表的逆置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
LinkList HeadInsert(LinkList &L){
InitList(L);
int x;
cin>>x;
while(x!=9999){
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = x;
s->next = L->next;
L->next = s;
cin>>x;
}
return L;
}
|
头插法是指在单链表的头部插入新节点的一种常见方法。在使用头插法插入元素时,最终链表中的数据顺序将与原始数据的顺序相反。
插入步骤
- **插入
A**:链表为空,将 A 设为头节点。
head -> A
- **插入
B**:将 B 插入到 A 之前。
head -> B -> A
- **插入
C**:将 C 插入到 B 之前。
head -> C -> B -> A
- **插入
D**:将 D 插入到 C 之前。
head -> D -> C -> B -> A
最终链表中的元素顺序为 D -> C -> B -> A,可见,这与原始插入顺序完全相反。
尾插法建立单链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
LinkList TailInsert(LinkList &L){
InitList(L);
LNode *s,*r=L;
int x;
cin>>x;
while(x!=9999){
s = (LNode *)malloc(sizeof(LNode));
s->data = x;
r->next = s;
r = s;
cin>>x;
}
r->next = NULL;
return L;
}
|
插入步骤
尾插法是指在单链表的末尾插入新节点。在使用尾插法插入元素时,链表中的数据顺序将与原始数据的顺序一致。具体步骤如下:
- **插入
A**:链表为空,将 A 设为头节点。
head -> A
- **插入
B**:找到最后一个结点 A,将 B 放到其后。
head -> A -> B
- **插入
C**:找到最后一个结点 B,将 C 放到其后。
head -> A -> B -> C
- **插入
D**:找到最后一个结点 C,将 D 放到其后。
head -> A -> B -> C -> D
最终链表中的元素顺序为 A -> B -> C -> D,与原始插入顺序一致。因此,尾插法更适合在需要保留插入数据顺序的场景下使用。
总结
- 头插法:得到的链表顺序与插入顺序相反。
- 尾插法:得到的链表顺序与插入顺序一致。
插入
时间复杂度=O(1)
带头结点的插入
1
2
3
4
5
6
|
bool Insert(LinkList &L, int i, int e){
if(i<1) return false;
LNode *p = GetElem(L,i-1);
return InsertNextNode(p, e);
}
|
不带头结点的插入
1
2
3
4
5
6
7
8
9
10
11
12
13
|
bool Insert(LinkList &L, int i, int e){
if(i<1) return false;
if(i==1){
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = e;
s->next = L;
L = s;
return true;
}
LNode *p = GetElem(L,i-1);
return InsertNextNode(p, e);
}
|
指定结点的后插操作
1
2
3
4
5
6
7
8
9
10
|
bool InsertNextNode(LNode *p, int e){
if(p==NULL) return false;
LNode *s = (LNode *)malloc(sizeof(LNode));
if(s==NULL) return false;
s->data = e;
s->next = p->next;
p->next = s;
return true;
}
|
指定结点的前插操作
还是插在p后面,只不过让p和插入结点的值交换
1
2
3
4
5
6
7
8
9
10
11
|
bool InsertPriorNode(LNode *p, int e){
if(p==NULL) return false;
LNode *s = (LNode *)malloc(sizeof(LNode));
if(s==NULL) return false;
s->next = p->next;
p->next = s;
s->data = p->data;
p->data = e;
return true;
}
|
删除
按位序删除
1
2
3
4
5
6
7
8
9
10
11
|
bool Delete(LinkList &L, int i int &e){
if(i<1 || i>Length(L))
return false;
LNode *p = GetElem(L,i-1);
LNode *q = p->next;
e = q->data;
p->next = q->next;
free(q);
return true;
}
|
按位序删除的时间复杂度:
最好情况:删除第一个,不需查找位置,循环0次,最好时间复杂度=O(1)
最坏情况:删除最后一个,需查找第n位,循环n次,最坏时间复杂度=O(n)
平均情况:删除任意一个,平均时间复杂度=O(n)
指定结点的删除
时间复杂度=O(n)
方法:p的后一个为q,p指向q的下一个,把q的值给p,最后释放q
1
2
3
4
5
6
7
8
9
|
bool Delete(LNode *p){
if(p==NULL) return false;
LNode *q = p->next;
p->data = q->data
p->next = q->next;
free(q);
return true;
}
|
查找
按位查找
平均时间复杂度=O(n)
1
2
3
4
5
6
7
8
9
10
11
|
LNode *GetElem(LinkList L, int i){
int j=0;
LNode *p = L;
if(i<0) return NULL;
while(p && j<i){
p = p->next;
j++;
}
return p;
}
|
按值查找
平均时间复杂度=O(n)
1
2
3
4
5
6
7
8
|
LNode *LocateElem(LinkList L, int e){
LNode *p = L->next;
while(p && p->data != e){
p = p->next;
}
return p;
}
|
求表长
平均时间复杂度=O(n)
1
2
3
4
5
6
7
8
9
10
|
int Length(LinkList L){
int len = 0;
LNode *p = L;
while(P->next){
p = p->next;
len++;
}
return len;
}
|
遍历
1
2
3
4
5
6
7
8
9
|
void PrintList(LinkList L){
LNode *p = L->next;
while(p){
cout<<p->data<<" ";
p = p->next;
}
cout<<endl;
}
|
五、完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
| #include<bits/stdc++.h>
using namespace std;
typedef struct LNode{
int data;
struct LNode *next;
}LNode, *LinkList;
void InitList(LinkList &L){
L = (LNode *)malloc(sizeof(LinkList));
L->next = NULL;
}
void PrintList(LinkList L){
LNode *p = L->next;
while(p){
cout<<p->data<<" ";
p = p->next;
}
cout<<endl;
}
int Length(LinkList L){
LNode *p = L->next;
int len = 0;
while(p){
len++;
p = p->next;
}
return len;
}
LinkList HeadInsert(LinkList &L){
InitList(L);
int x;
cin>>x;
while(x!=9999){
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = x;
s->next = L->next;
L->next = s;
cin>>x;
}
return L;
}
LinkList TailInsert(LinkList &L){
InitList(L);
LNode *s,*r=L;
int x;
cin>>x;
while(x!=9999){
s = (LNode *)malloc(sizeof(LNode));
s->data = x;
r->next = s;
r = s;
cin>>x;
}
r->next = NULL;
return L;
}
LNode *LocateElem(LinkList L, int x){
LNode *p = L->next;
while(p && p->data != x){
p = p->next;
}
return p;
}1
LNode *GetElem(LinkList L, int i){
int j=1;
LNode *p = L->next;
if(i==0)return L;
if(i<1)return NULL;
while(p && j<i){
p = p->next;
j++;
}
return p;
}
void Insert(LinkList &L, int i, int x){
LNode *p = GetElem(L,i-1);
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = x;
s->next = p->next;
p->next = s;
}
void Delete(LinkList &L, int i){
if(i<1 || i>Length(L)){
cout<<"delete failed: index is wrong."<<endl;
return;
}
LNode *p = GetElem(L,i-1);
LNode *q = p->next;
p->next = q->next;
free(q);
}
int main(){
LinkList L = TailInsert(L);
Insert(L,2,888);
cout<<"在第二个位置插入888: ";
PrintList(L);
Delete(L,4);
cout<<"删除第四个结点后:";
PrintList(L);
LNode *p = GetElem(L,3);
cout<<"第三个结点的值为:"<<p->data<<endl;
LNode *q = LocateElem(L,2);
cout<<"数据为2的结点的下一个结点的值为:"<<q->next->data<<endl;
cout<<"单链表的长度:"<<Length(L)<<endl;
return 0;
}
|
双链表—— Double Linked List
一、单链表的定义
单链表的结点中只有一个指向其后继的指针,使得单链表要访问某个结点的前驱结点时,只能从头开始遍历,访问后驱结点的复杂度为O(1),访问前驱结点的复杂度为O(n)。为了克服上述缺点,引入了双链表。
双链表的结点中有两个指针prior和next,分别指向前驱结点和后继结点。
二、双链表的实现方式
实现方式:不带头结点和带头结点,一般带头结点比不带头结点好
带头结点:写操作代码方便,一般用带头结点,不明确的都是带头结点的
不带头结点:写操作代码麻烦,要区分第一个数据和后续数据的处理
三、双链表上的操作(带头结点)
双链表的类型描述
1
2
3
4
| typedef struct DNode{
int data;
struct DNode *prior,*next;
}DNode, *DLinkList;
|
初始化
1
2
3
4
5
6
7
8
|
bool InitList(DLinkList &L){
L = (DNode *)malloc(sizeof(DLinkList));
if(L == NULL) return false;
L->prior = NULL;
L->next = NULL;
return true;
}
|
判空
1
2
3
4
5
6
7
8
|
bool Empty(DLinkList L){
if(L->next == NULL){
return true;
}else{
return false;
}
}
|
建立双链表
头插法建立双链表
用于链表的逆置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
DLinkList HeadInsert(DLinkList &L){
InitList(L);
int x;
cin>>x;
while(x!=9999){
DNode *s = (DNode *)malloc(sizeof(DNode));
s->data = x;
if(L->next == NULL){
s->next = NULL;
s->prior = L;
L->next = s;
}else{
s->next = L->next;
L->next->prior = s;
s->prior = L;
L->next = s;
}
cin>>x;
}
return L;
}
|
尾插法建立单链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
DLinkList TailInsert(DLinkList &L){
InitList(L);
DNode *s,*r=L;
int x;
cin>>x;
while(x!=9999){
s = (DNode *)malloc(sizeof(DNode));
s->data = x;
s->next = NULL;
s->prior = r;
r->next = s;
r = s;
cin>>x;
}
return L;
}
|
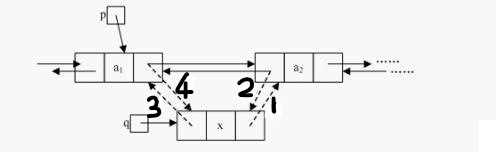
插入
时间复杂度=O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
bool Insert(DNode *p, int x){
DNode *s = (DNode *)malloc(sizeof(DNode));
if(p == NULL||s==NULL) return false;
s->data = x;
s->next = p->next;
if(p->next != NULL) p->next->prior = s;
s->prior = p;
p->next = s;
return true;
}
bool Insert(DNode *p, DNode *s){
if(p == NULL||s==NULL) return false;
s->next = p->next;
if(p->next != NULL) p->next->prior = s;
s->prior = p;
p->next = s;
return true;
}
|
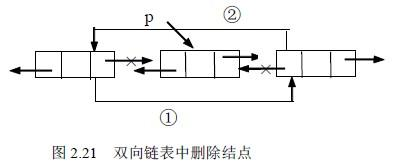
删除
按位序删除
时间复杂度=O(n)
1
2
3
4
5
6
7
8
9
10
11
|
bool Delete(DLinkList &L, int i){
if(i<1 || i>Length(L)) return false;
DNode *p = GetElem(L,i-1);
if(p == NULL) return false;
DNode *q = p->next;
p->next = q->next;
if(p->next != NULL) q->next->prior = p;
free(q);
return true;
}
|
指定结点的删除
时间复杂度=O(1)
1
2
3
4
5
6
7
8
9
|
void DeleteNextNode(DNode *p){
if(p == NULL) return false;
DNode *q = p->next;
if(q == NULL) return false;
p->next = q->next;
if(p->next != NULL) q->next->prior = p;
free(q);
}
|
查找(与单链表完全一样)
按位查找
平均时间复杂度=O(n)
1
2
3
4
5
6
7
8
9
10
11
|
DNode *GetElem(DLinkList L, int i){
int j=0;
DNode *p = L;
if(i<0) return NULL;
while(p && j<i){
p = p->next;
j++;
}
return p;
}
|
按值查找
平均时间复杂度=O(n)
1
2
3
4
5
6
7
8
|
DNode *LocateElem(DLinkList L, int e){
DNode *p = L->next;
while(p && p->data != e){
p = p->next;
}
return p;
}
|
求表长(与单链表完全一样)
平均时间复杂度=O(n)
1
2
3
4
5
6
7
8
9
10
|
int Length(DLinkList L){
int len = 0;
DNode *p = L;
while(P->next){
p = p->next;
len++;
}
return len;
}
|
遍历(与单链表完全一样)
1
2
3
4
5
6
7
8
9
|
void PrintList(DLinkList L){
DNode *p = L->next;
while(p){
cout<<p->data<<" ";
p = p->next;
}
cout<<endl;
}
|
销毁
1
2
3
4
5
6
7
8
9
|
void DestoryList(DLinkList L){
while(L->next != NULL){
DeleteNextNode(L);
}
free(L);
L = NULL;
}
|
四、完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
| #include<bits/stdc++.h>
using namespace std;
typedef struct DNode{
int data;
struct DNode *prior,*next;
}DNode, *DLinkList;
void InitList(DLinkList &L){
L = (DNode *)malloc(sizeof(DLinkList));
L->prior = NULL;
L->next = NULL;
}
void PrintList(DLinkList L){
DNode *p = L->next;
while(p){
cout<<p->data<<" ";
p = p->next;
}
cout<<endl;
}
int Length(DLinkList L){
DNode *p = L->next;
int len = 0;
while(p){
len++;
p = p->next;
}
return len;
}
DLinkList HeadInsert(DLinkList &L){
InitList(L);
int x;
cin>>x;
while(x!=9999){
DNode *s = (DNode *)malloc(sizeof(DNode));
s->data = x;
if(L->next == NULL){
s->next = NULL;
s->prior = L;
L->next = s;
}else{
s->next = L->next;
L->next->prior = s;
s->prior = L;
L->next = s;
}
cin>>x;
}
return L;
}
DLinkList TailInsert(DLinkList &L){
InitList(L);
DNode *s,*r=L;
int x;
cin>>x;
while(x!=9999){
s = (DNode *)malloc(sizeof(DNode));
s->data = x;
s->next = NULL;
s->prior = r;
r->next = s;
r = s;
cin>>x;
}
return L;
}
DNode *LocateElem(DLinkList L, int x){
DNode *p = L->next;
while(p && p->data != x){
p = p->next;
}
return p;
}
DNode *GetElem(DLinkList L, int i){
int j=1;
DNode *p = L->next;
if(i==0)return L;
if(i<1)return NULL;
while(p && j<i){
p = p->next;
j++;
}
return p;
}
void Insert(DLinkList &L, DNode *p, int x){
DNode *s = (DNode *)malloc(sizeof(DNode));
s->data = x;
s->next = p->next;
p->next->prior = s;
s->prior = p;
p->next = s;
}
void Delete(DLinkList &L, int i){
if(i<1 || i>Length(L)){
cout<<"delete failed: index is wrong."<<endl;
return;
}
DNode *p = GetElem(L,i-1);
DNode *q = p->next;
p->next = q->next;
q->next->prior = p;
free(q);
}
bool Empty(DLinkList L){
if(L->next == NULL){
cout<<"L is null"<<endl;
return true;
}else{
cout<<"L is not null"<<endl;
return false;
}
}
int main(){
DLinkList L = TailInsert(L);
cout<<"L: ";
PrintList(L);
DNode *p;
p = LocateElem(L,2);
cout<<"值为2的结点的下一个结点值是:"<<p->next->data<<endl;
cout<<"值为2的结点的上一个结点值是:"<<p->prior->data<<endl;
p = GetElem(L,3);
cout<<"第三个结点值是:"<<p->data<<endl;
Insert(L,p,7);
cout<<"在第三个结点后面插入值为7的结点后L: ";
PrintList(L);
Delete(L, 5);
cout<<"删除第五个结点后L: ";
PrintList(L);
cout<<"表长为:"<<Length(L)<<endl;;
Empty(L);
return 0;
}
|
栈—— Stack
一、栈的定义
栈是线性表结构的一种,但是栈结构的插入与删除操作都只能从同一端进行,所以栈结构是一种受限制的线性表结构,数据的插入与删除符合LIFO的原则(也就是后进先出,先进后出)。
二、栈的基本操作
注:参数代“&”表示:方法运行完后,对参数修改的结果要“带回来”
对数据的操作:创销,增删查改
1
2
3
4
5
6
7
8
9
10
| InitStack(&S);
DestoryStack(&S);
Push(&S,x);
Pop(&S,&x);
GetTop(S,&x);
StackEmpty(S);
|
三、存储结构
顺序存储和链式存储
四、栈分类
栈的顺序存储:顺序栈
栈的链式存储:链栈
顺序栈—— Sequence Stack
一、顺序栈的定义
顺序栈:栈的顺序存储。
二、顺序栈的实现方式
实现方式:静态分配和动态分配
三、静态分配的顺序栈上的操作
顺序栈的类型描述
1
2
3
4
5
| #define MaxSize 10
typedef struct{
Elemtype data[MaxSize];
int top;
}SqStack;
|
初始化
1
2
3
4
|
void InitStack(SqStack &S){
S.top = -1;
}
|
判栈空
1
2
3
4
5
6
7
| bool StackEmpty(SqStack S){
if(S.top == -1){
return true;
}else{
return false;
}
}
|
入栈
1
2
3
4
5
6
7
|
bool Push(SqStack &S,Elemtype e){
if(S.Top == MaxSize-1) return false;
S.Top = S.Top + 1;
S.data[S.top] = e;
return true;
}
|
出栈
1
2
3
4
5
6
7
|
bool Pop(Stack &S,Elemtype &e){
if(S.Top == -1) return false;
e = S.data[S.Top];
S.Top = S.Top - 1;
return true;
}
|
获取栈顶元素
1
2
3
4
5
6
|
bool GetTop(Stack &S,Elemtype &e){
if(S.Top==S.Base) return false;
e = S.data[S.Top];
return true;
}
|
四、动态分配的顺序栈上的操作
顺序栈的类型描述
1
2
3
4
5
| typedef struct Stack{
Elemtype *Top;
Elemtype *Base;
int stacksize;
}SqStack
|
初始化
1
2
3
4
5
6
7
8
|
bool InitStack(SqStack &S){
S.Base=(Elemtype *)malloc(MAXSIZE*sizeof(Elemtype));
if(!S.Base) return false;
S.Top=S.Base;
S.stacksize=MAXSIZE;
return true;
}
|
判栈空
1
2
3
4
5
6
7
| bool StackEmpty(SqStack S){
if(S.Top == S.Base){
return true;
}else{
return false;
}
}
|
入栈
1
2
3
4
5
6
7
|
bool Push(SqStack &S,Elemtype e){
if(S.Top-S.Base==S.stacksize) return false;
*S.Top=e;
S.Top++;
return true;
}
|
出栈
1
2
3
4
5
6
|
bool Pop(Stack &S,Eletype &x){
if(S.Top==S.Base) return false;
x=*--S.Top;
return true;
}
|
获取栈顶元素
1
2
3
4
5
6
|
bool GetTop(Stack &S,Elemtype &e){
if(S.Top==S.Base) return false;
e = *(S.Top-1);
return true;
}
|
链栈—— Linked Stack
一、链栈的定义
链栈:栈的链式存储。
二、链栈的实现方式
实现方式:不带头结点和带头结点,一般带头结点比不带头结点好
不带头结点:写操作代码麻烦,要区分第一个数据和后续数据的处理
带头结点:写操作代码方便,一般用带头结点,不明确的都是带头结点的
注:这两种方式:只有类型描述一样,初始化不一样,
判空、入栈、出栈、取栈顶元素不一样,不带头节点是s,带头结点是s->next,因为链栈以链头为栈顶
三、不带头结点的链栈上的操作(与不带头结点的单链表一样)
链头为栈顶
链栈的类型描述
1
2
3
4
| typedef struct LNode{
int data;
struct LNode *next;
}LNode, *LinkStack;
|
初始化
1
2
3
4
5
|
void InitStack(LinkStack &S){
S = NULL;
S->next = NULL;
}
|
判栈空
1
2
3
4
5
6
7
8
|
bool StackEmpty(LinkStack S){
if(S == NULL){
return true;
}else{
return false;
}
}
|
入栈(与单链表插入一样)
1
2
3
4
5
6
7
8
9
10
| bool push(LNode *s, int x){
if(s==NULL) return false;
LNode *p = (LNode*)malloc(sizeof(LNode));
if(p==NULL) return false;
p->next = NULL;
p->data = x;
p->next = s;
s = p;
return true;
}
|
出栈(与单链表删除一样)
1
2
3
4
5
6
7
8
| bool Delete(LNode *s){
if(s==NULL) return false;
LNode *q = s;
s->data = q->data
s = q->next;
free(q);
return true;
}
|
获取栈顶元素(与单链表删除一样)
1
2
3
4
5
6
|
bool GetTop(LNode &s,Elemtype &e){
if(s == NULL) return false;
e = s->data;
return true;
}
|
四、带头结点的链栈上的操作
s都改为s->next,类型描述和初始化例外
链栈的类型描述
1
2
3
4
| typedef struct LNode{
int data;
struct LNode *next;
}LNode, *LinkStack;
|
初始化
1
2
3
4
5
|
void InitStack(LinkStack &S){
S = (LNode*)malloc(sizeof(LNode));
S->next = NULL;
}
|
判栈空
1
2
3
4
5
6
7
| bool StackEmpty(LinkStack S){
if(S->next == NULL){
return true;
}else{
return false;
}
}
|
入栈(与单链表插入一样)
1
2
3
4
5
6
7
8
9
10
| bool push(LNode *s, int x){
if(s==NULL) return false;
LNode *p = (LNode*)malloc(sizeof(LNode));
if(p==NULL) return false;
p->next = NULL;
p->data = x;
p->next = s->next;
s->next = p;
return true;
}
|
出栈(与单链表删除一样)
1
2
3
4
5
6
7
8
| bool Delete(LNode *s){
if(s==NULL) return false;
LNode *q = s->next;
s->data = q->data
s->next = q->next;
free(q);
return true;
}
|
获取栈顶元素
1
2
3
4
5
6
|
bool GetTop(LNode &s,Elemtype &e){
if(s->next == NULL) return false;
e = s->next->data;
return true;
}
|



